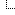(08-15-2018, 01:03 PM)Millan Wrote: O tome sam i ja pričao, jer sam još juče pripremio par sličica za objašnjenje paradoksa. Na ovoj sličici vide se dve tačke, donja (P) i gornja (P´). Tačka P je nepokretna u tom trenutku, jer je ona oslonac tela koje se kotrlja, a ne proklizava. S obzirom da je nepokretna ona je u tom trenutku (a svakog drugog trenutka dolazi neka druga tačka u taj položaj) tačka rotacije tog tela. Iz toga je očigledno da imamo složeno kretanje: rotaciju i translaciju. Zato sam se iznenadio kad sam video da se ubacuje i klizanje, kog definitivno nema, ali to smo raspravili u prethodnom postu. Ali i dalje nemamo odgovor: zašto nam se čini da su kretanja tački na različitim poluprečnicima ista, odnosno kako to da je 3 jednako 5...To nam se dešava jer nismo definisali koordinatni sistem (lokaciju posmatrača) u kome analiziramo kretanje. Ako sedim na osovini točka, onda vidim samo njegovu rotaciju i različite tangencijalne brzine u radijalnom pravcu, a podloga se kreće u odnosu na mene translatornom brzinom centra točka.
Slično je i sa trenažerom za trčanje - traka se kreće, a osoba na njoj je stacionarna, ali je sa aspekta relativnog kretanja trake i osobe probelm u oba slučaja isti.
Ako pak stojim na ivici puta i posmatram točak, onda će svaka tačka na točku imati različitu brzinu u odnosu na mene. Na primer, ako izaberem jednu tačku na obodu i pratim je, ona će za jedan obrtaj točka opisati cikloidu. Ako tačku koju pratim pomeram prema centru točka, cikloida postaje sve plića i u centru vidim samo translatorno kretanje.
Matematički izraženo, brzina svake tačke točka u svakom trenutku vremena je vektorski zbir čiste translacije i čiste rotacije, kao što prikazuje tvoja skica.
Pozdrav